Scatter Plot
A scatter plot is also known to be called as a scatter graph, scatterplot, scatter chart, scatter diagram or scattergram. It is a type of a plot or mathematical diagram and to make it the Cartesian coordinates can be used for displaying the numeral values for usually two variables for one set of data.
In case the points are colour-coded, then one variable can be displayed in addition. The data that are being displayed is represented as a collection of points, each of which has the value of one variable determining the position on the horizontal axis. Another value of the other variable is known to be determining the position on the vertical axis within a scatter plot.

Example 1. Scatter Plot — 2^x function
A scatter plot can be used when one continuous variable that is controlled by the experimenter and the other depends on it or when both of the continuous variables are independent. In case some of the parameters that exist is being systematically decremented andor incremented by the others, then it is known to be called as a “control parameter” or an “independent variable” being customarily plotted all the way along the horizontal axis.
The so-called dependent or measured variable is known to be customarily plotted all along the vertical axis. In case there is no dependent variable that exists, then any type of variable can be plotted on any axis and a scatter plot can illustrate only a degree of correlation between two of the variables.
In statistics, association or dependence is any statistical relationship, whether it is causal or not, between bivariate data or two variables. Correlation is known to be any of a broad class of the statistical relationships that involves dependence. Although, in a common usage, a correlation usually can be referred to how close two variables are for having a linear relationship with each other.
The familiar examples of the dependent phenomena may include the correlation between the demand for a product and its price, for example.
Correlations are known to be very useful because they can indicate some predictive relationship that can be exploited in practice. An electrical utility may produce less power on a mild day being based on the correlation between weather and electricity demand. In this example of a causal relationship, because of the extreme weather conditions, people may use more electricity for either cooling or heating. Although, usually, the presence of some correlation is known to be insufficient for inferring the presence of some causal relationship.
The random variables are known to be dependent in case they cannot satisfy some mathematical property of the probabilistic independence. The correlation in informal parlance is simply synonymous with dependence. Although, being used in a technical sense, a correlation may be referring to any of a few specific types of relationship between different mean values.

Example 2. Scatter Plot — Widgets price scatter
There are a few correlation coefficients used measuring the degree of correlation. The most common is the so-called “Pearson correlation coefficient” — the sensitive only to a linear relationship between two variables one. Other correlation coefficients are known to have been developed in order to be more robust than the mentioned Pearson correlation. By the way, any mutual information can also be applied for measuring the dependence between two variables.
A scatter plot can suggest many different kinds of correlations between different variables with some certain confidence interval. Weight and height, for example, height would be on the x-axis and weight would be on y-axis. Correlations may be either positive (or “rising”), negative (or “falling”), or null (or simply “uncorrelated”). In case the pattern of dots slopes from lower left to upper right, then it can indicate a positive correlation between the variables being studied.
A line of best fit that is known to be also called as a “trendline” can be drawn for being used to study the relationship between different variables. An equation for any correlation between different variables can be determined by the established best-fit procedures.
For any linear correlation, the best procedure is the so-called “linear regression”. The mentioned regression can be guaranteed one for generating some correct solution in a finite time. There is no universal best-fit procedure that is guaranteed for generating a correct solution for any arbitrary relationships. A scatter plot that can be created with the help of ConceptDraw DIAGRAM and so the Scatter Diagrams solution can be also very useful when we want to see the way how two comparable data sets agree to show the so-called “nonlinear relationships” between different variables.
The scatter diagram can be also used as one of the seven basic tools of quality control and the scatter charts can be built in the form of a marker, bubble or/and line charts either with the aid of the pre-designed templated that are provided in the Scatter Diagrams solution or from a scratch.

Example 3. Scatter Plot — Cars price depending on age
A so-called “generalized scatter plot matrix” can also be created in ConceptDraw DIAGRAM diagramming and drawing application, knowing to be offering a range of displays of the paired combinations of both quantitative and categorical variables. A fluctuation diagram, faceted bar chart or a mosaic plot may be all used for displaying two different categorical variables. Other plots can be used for one quantitative and one categorical variables.
SIX RELATED HOW TO's:
A pie chart or a circle graph is a circular chart divided into sectors, illustrating numerical proportion. In a pie chart, the arc length of each sector and consequently its central angle and area, is proportional to the quantity it represents.
Pie chart examples and templates created using ConceptDraw DIAGRAM software helps you get closer with pie charts and find pie chart examples suite your needs.
Picture: Pie Chart Examples and Templates
Related Solution:
Need to draw a diagram, process chart, flowchart, organizational chart, graphic design? ConceptDraw can help you to make professional graphic documents quickly.
Picture: Best Diagramming
Related Solution:
As restaurant industry is growing rapidly nowadays, researches show that almost half of the adults have worked in a restaurant or a cafe. Moreover, many of them dream to start their own someday. Unfortunately, it takes a lot of time to write a business plan and to find a great location, although some know how to create a restaurant floor plan in minutes or how to plan budget effortlessly. Hiring employees can also cause a lot of headache, but this is crucial for further success, because every guest comes to restaurant for a good service and delicious food. It is also worth noting that restaurant concept is also important, because it defines target audience and influences the menu.
This diagram represents the floor plan of an ongoing sports-theme establishment - restaurant, cafe, or other food service. A number of widescreen monitors installed along the perimeter provide visitors the opportunity to follow the course of a match from anywhere in the dining room of restaurant or cafe. The most of sports fans believe that food and alcohol is a big part of any sports show. That is why the dining room takes the most space - almost 60% of the total establishment space. Nearly all sports fans consume beverages while watching sports - beer, soda or water at least. Thus, the restaurant floor plan designers added a large lavatory there. Moreover, project developers considered unnecessary the gender division of such delicate place - perhaps they guess that only men are watching football, or believe that alcohol will eliminate the most of gender differences.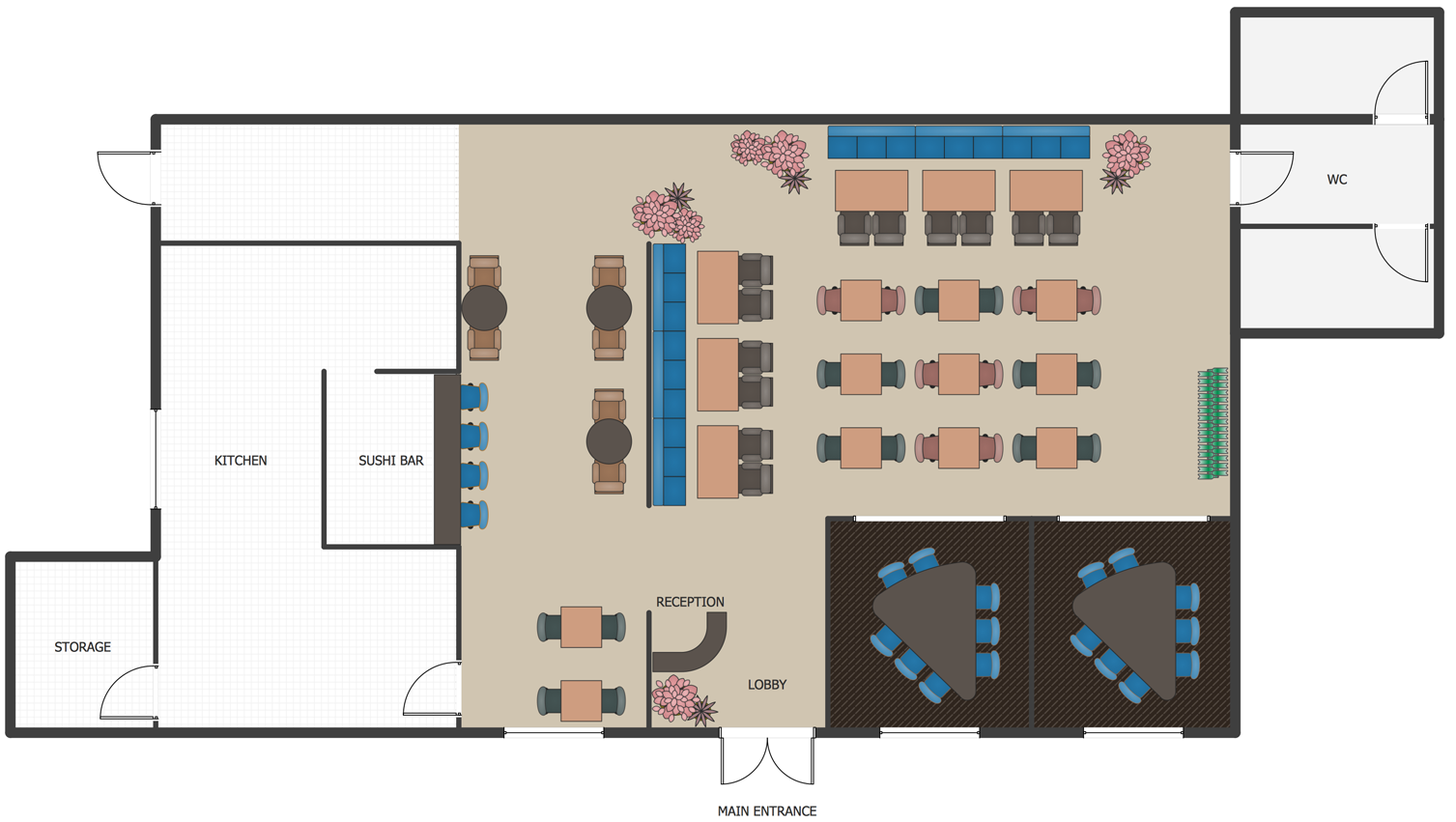
Picture: How To Create Restaurant Floor Plan in Minutes
Related Solution:
The behavior of worker in organization is influences organizational effectiveness. A simple block diagram made with ConceptDraw Block diagrams solution can improve the understanding of expectations of workers regarding what they l contribute to organization and what they wait to obtain. Making block diagram depicting the individual behavior in organization is used in HR management to obtain an optimal and positive overall contribution to the organization.
The behavior of worker in organization is influences organizational effectiveness. A simple block diagram made with ConceptDraw Block diagrams solution can improve the understanding of expectations of workers regarding what they l contribute to organization and what they wait to obtain. Making block diagram depicting the individual behavior in organization is used in HR management to obtain an optimal and positive overall contribution to the organization.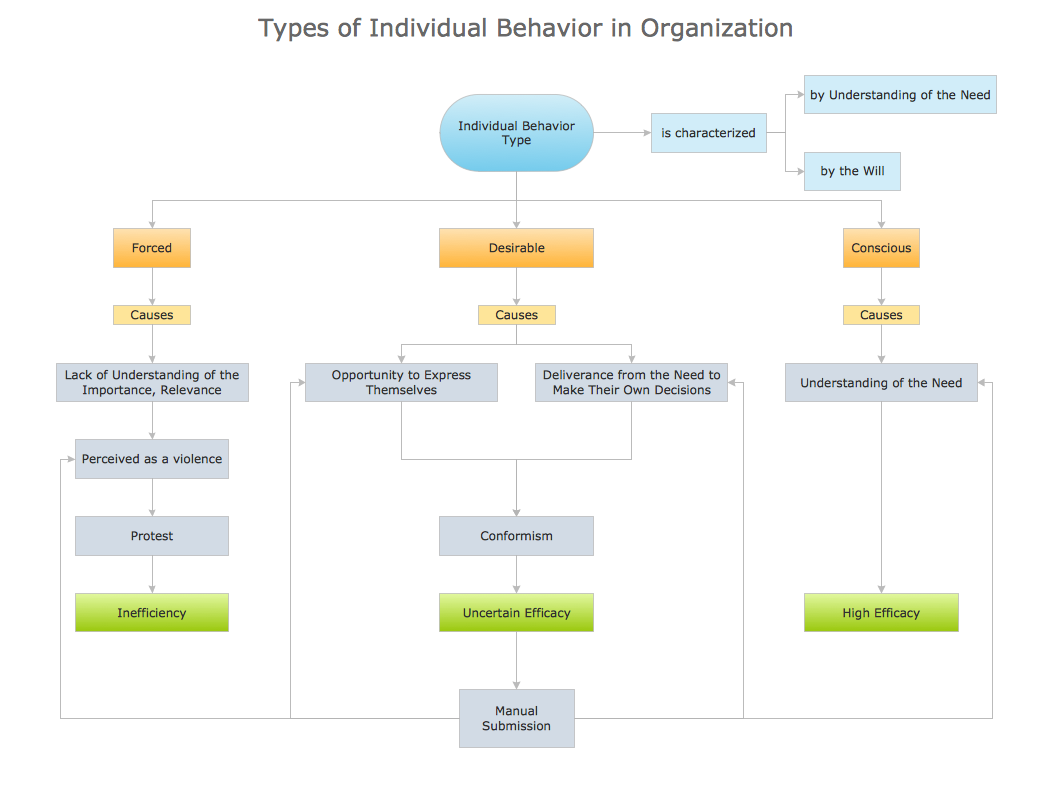
Picture: Basic Diagramming
Related Solution:
When trying to figure out the nature of the problems occurring within a project, there are many ways to develop such understanding. One of the most common ways to document processes for further improvement is to draw a process flowchart, which depicts the activities of the process arranged in sequential order — this is business process management. ConceptDraw DIAGRAM is business process mapping software with impressive range of productivity features for business process management and classic project management. This business process management software is helpful for many purposes from different payment processes, or manufacturing processes to chemical processes. Business process mapping flowcharts helps clarify the actual workflow of different people engaged in the same process. This samples were made with ConceptDraw DIAGRAM — business process mapping software for flowcharting and used as classic visio alternative because its briefly named "visio for mac" and for windows, this sort of software named the business process management tools.
This flowchart diagram shows a process flow of project management. The diagram that is presented here depicts the project life cycle that is basic for the most of project management methods. Breaking a project into phases allows to track it in the proper manner. Through separation on phases, the total workflow of a project is divided into some foreseeable components, thus making it easier to follow the project status. A project life cycle commonly includes: initiation, definition, design, development and implementation phases. Distinguished method to show parallel and interdependent processes, as well as project life cycle relationships. A flowchart diagram is often used as visual guide to project. For instance, it used by marketing project management software for visualizing stages of marketing activities or as project management workflow tools. Created with ConceptDraw DIAGRAM — business process mapping software which is flowcharting visio alternative or shortly its visio for mac, this sort of software platform often named the business process management tools.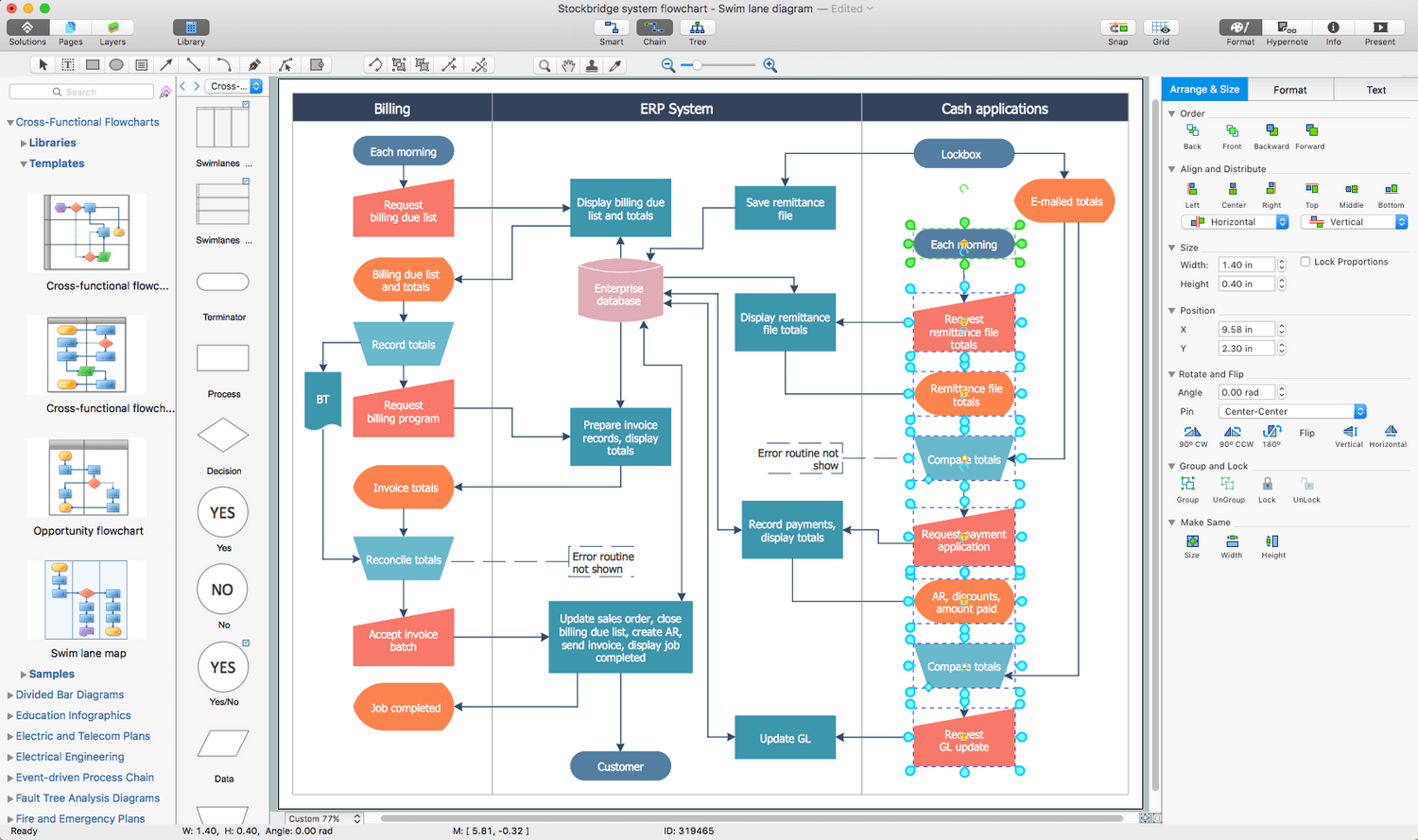
Picture: Process Flowchart
Related Solution:
Tips on how to make an accounting flowchart. Describing methods and symbols that are used to represent the accounting system.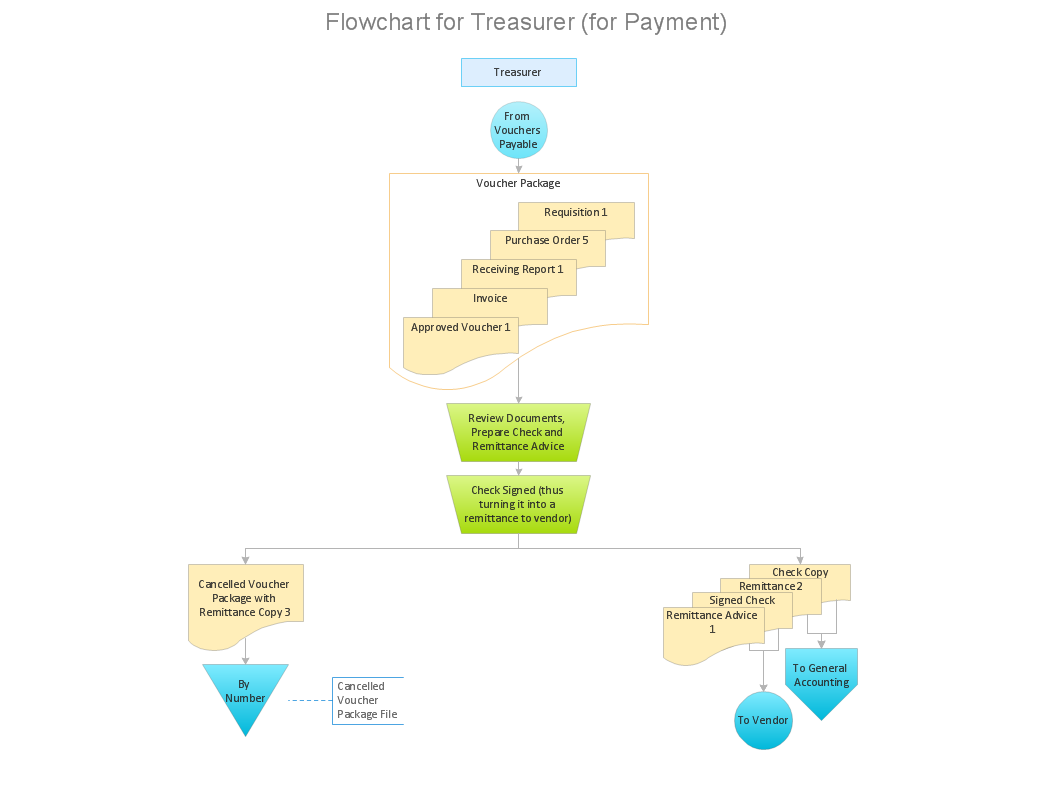
Picture: How to Make an Accounting Process Flowchart
Related Solution:








