Products Solutions Samples Buy
✕
This site uses cookies. By continuing to browse the ConceptDraw site you are agreeing to our Use of Site Cookies.
Try ConceptDraw Free
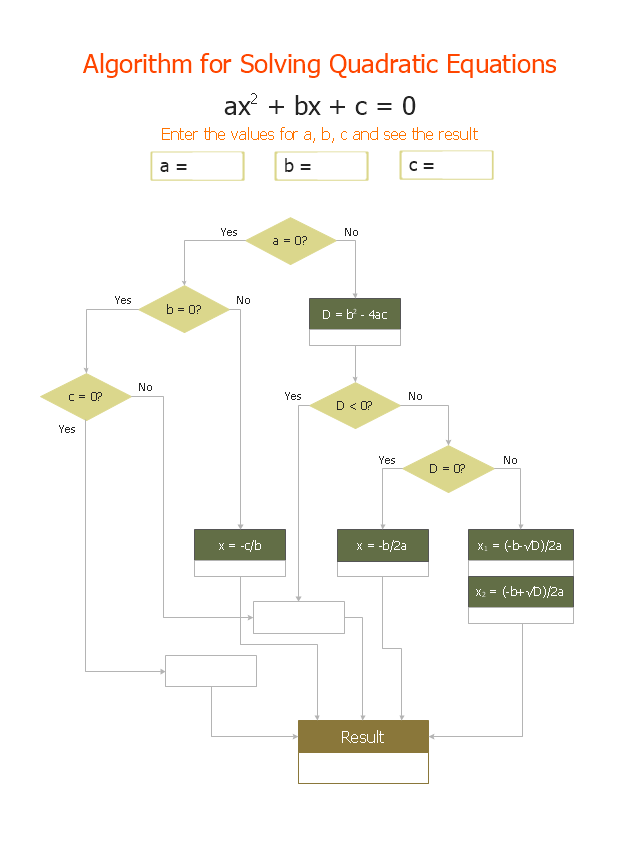
"In elementary algebra, a quadratic equation (from the Latin quadratus for "square") is any equation having the form
ax^2+bx+c=0
where x represents an unknown, and a, b, and c are constants with a not equal to 0. If a = 0, then the equation is linear, not quadratic. The constants a, b, and c are called, respectively, the quadratic coefficient, the linear coefficient and the constant or free term.
Because the quadratic equation involves only one unknown, it is called "univariate". The quadratic equation only contains powers of x that are non-negative integers, and therefore it is a polynomial equation, and in particular it is a second degree polynomial equation since the greatest power is two.
Quadratic equations can be solved by a process known in American English as factoring and in other varieties of English as factorising, by completing the square, by using the quadratic formula, or by graphing." [Quadratic equation. Wikipedia]
The flowchart example "Solving quadratic equation algorithm" was created using the ConceptDraw PRO diagramming and vector drawing software extended with the Mathematics solution from the Science and Education area of ConceptDraw Solution Park.
Solving quadratic equation flow chart
Solving quadratic equation flow chart, rectangle,
Used Solutions

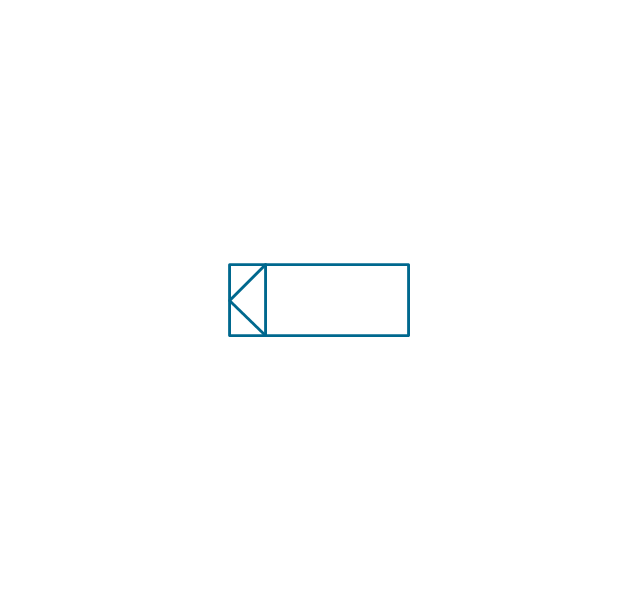
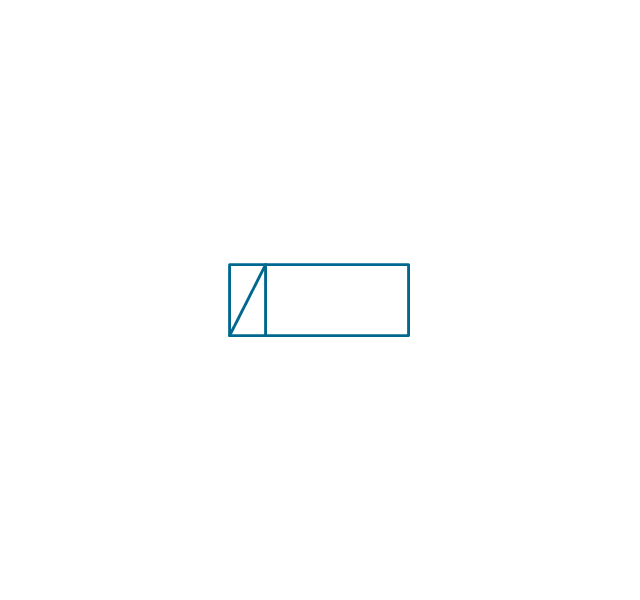
The vector stencils library "Switches and relays" contains 58 symbols of electrical contacts, switches, relays, circuit breakers, selectors, connectors, disconnect devices, switching circuits, current regulators, and thermostats for electrical devices.
Use these shapes for drawing electrical diagrams in the ConceptDraw PRO diagramming and vector drawing software extended with the Electrical Engineering solution from the Engineering area of ConceptDraw Solution Park.
www.conceptdraw.com/ solution-park/ engineering-electrical
SPST
SPST, SPST, single-pole, single-throw, switch,
SPDT
SPDT, SPDT, single-pole, double-throw, switch,
DPST
DPST, DPST, double-pole, single-throw, switch,
DPDT
DPDT, DPDT, double-pole, double-throw, switch,
Make contact
Make contact, make contact,
Break contact
Break contact, break contact,
Two way contact
Two way contact, two way contact,
Passing make-contact
Passing make-contact, passing make-contact,
Spring return
Spring return, spring return,
Stay put
Stay put, stay put, contact without spring return,
Limit switch
Limit switch, limit switch,
Circuit breaker
Circuit breaker, circuit breaker,
Spring return 2
Spring return 2, spring return, make,
Spring return 3
Spring return 3, spring return, break,
Limit switch n/o
Limit switch n/o, limit switch, directly actuated, spring returned, normally open,
Limit switch n/c
Limit switch n/c, limit switch, directly actuated, spring returned, normally closed,
2 position switch
2 position switch, 2 position, switch,
3 position switch
3 position switch, 3 position, three-position, switch,
4 position switch
4 position switch, 4 position, switch,
Manual switch
Manual switch, manual switch, manually operated switch,
Pushbutton make
Pushbutton make, pushbutton, make, circuit closing, mushroom head, push-pull head,
Pushbutton break
Pushbutton break, pushbutton, break, circuit opening, mushroom head, push-pull head,
Pushbutton 2-circuit
Pushbutton 2-circuit, pushbutton, 2-circuit, circuit opening, break,
Selector switch
Selector switch, selector switch, break-before-make, nonshorting, nonbridging, contact transfer,
Shorting selector
Shorting selector, shorting selector, make-before-break, shorting, bridging, contact transfer,
Proximity limit switch
Proximity limit switch, proximity limit switch, directly actuated, spring returned, normally closed,
Time delay make
Time delay make, time delay make, open switch, time-delay closing, TDC,
Time delay break
Time delay break, time delay break, closed switch, time-delay opening, TDO,
Time delay make 2
Time delay make 2, time delay make, normally open,
Time delay break 2
Time delay break 2, time delay break, normally closed,
Safety interlock
Safety interlock, safety interlock, circuit opening,
Flow actuated
Flow actuated, flow actuated,
Liquid level actuated
Liquid level actuated, liquid level actuated switch,
Liquid level actuated 2
Liquid level actuated 2, liquid level actuated switch,
Gas flow actuated
Gas flow actuated, gas flow actuated switch,
Pressure actuated
Pressure actuated, pressure actuated switch,
Temperature actuated
Temperature actuated, temperature actuated switch,
Thermostat
Thermostat, thermostat,
Temperature switch
Temperature switch, temperature switch, temperature sensitive switch,
Inertia switch
Inertia switch, inertia switch,
Mercury switch
Mercury switch, mercury switch,
Mercury switch 2
Mercury switch 2, mercury switch,
Fuse
Fuse, fuse,
Switch disconnector
Switch disconnector, switch disconnector, isolating-switch,
Isolator
Isolator, isolator,
Change-over contact
Change-over contact, change-over contact,
Relay contacts
Relay contacts, relay contacts,
Relay coil
Relay coil, relay coil,
Pilot light
Pilot light, pilot light,
Pilot light, push-to-test
Pilot light, push-to-test, pilot light,
Relay, alternating-current
Relay, alternating-current, relay,
Relay, magnetically polarized
Relay, magnetically polarized, relay,
Relay, slow-operate
Relay, slow-operate, relay,
Relay, slow-release
Relay, slow-release, relay,
Relay
Relay, relay,
Relay, high speed
Relay, high speed, relay,
Relay, mechanically latched
Relay, mechanically latched, relay,
Relay, permanent
Relay, permanent, relay,
Used Solutions
HelpDesk

How to Draw a Chemical Process Flow Diagram

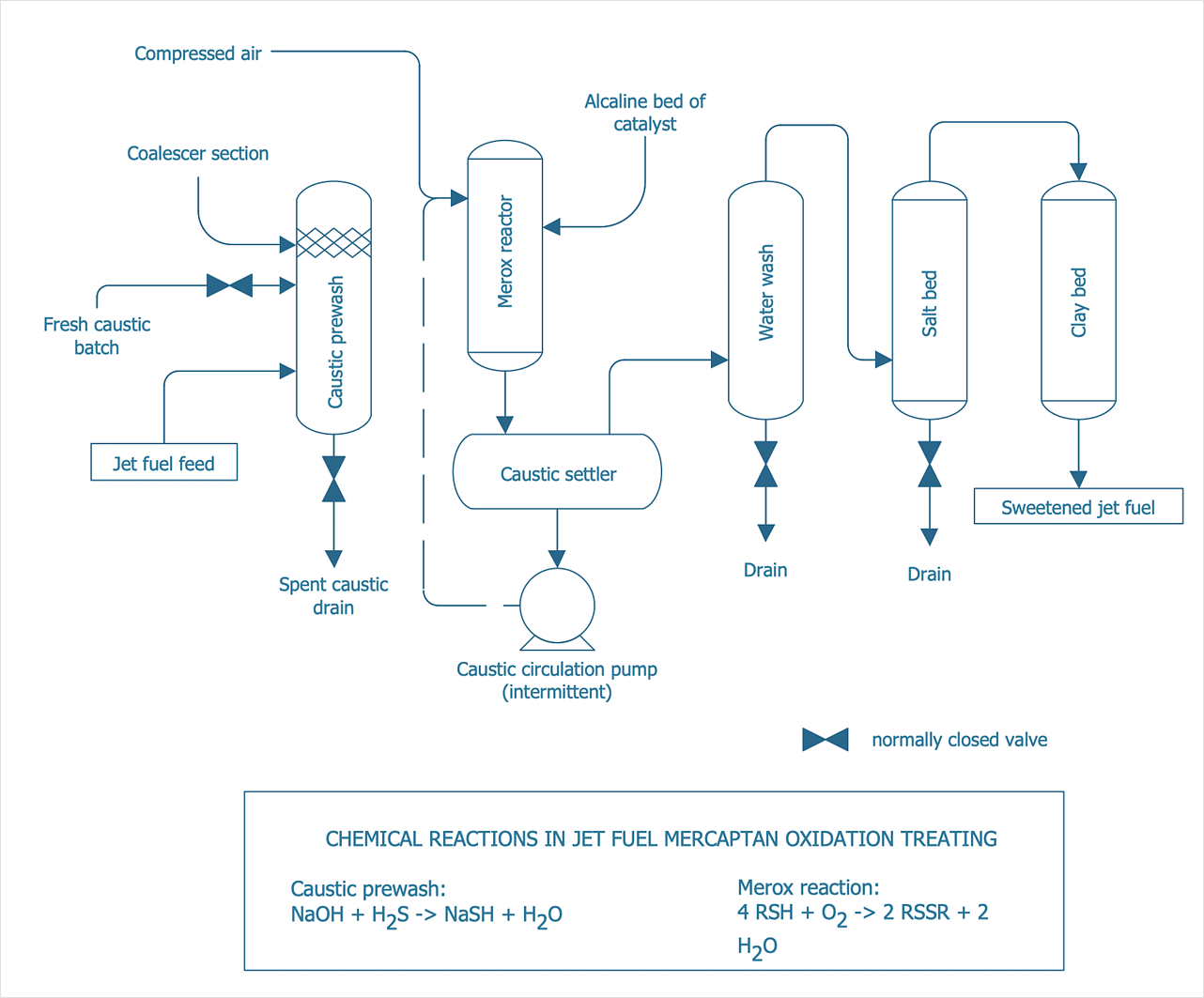
How to Draw a Chemical Process Flow Diagram
Process Flow Diagram widely used in modeling of processes in the chemical industry. A Chemical Process Flow diagram (PFD) is a specialized type of flowchart. With the help of Chemical Process Flow Diagram engineers can easily specify the general scheme of the processes and chemical plant equipment. Chemical Process Flow Diagram displays the real scheme of the chemical process, the relationship between the equipment and the technical characteristics of the process. Chemical Process Flow Diagram illustrates the connections between the basic equipment as well as the overall structure of pipelines and other supporting equipment. The purpose of the PFD is to build the image of the basic idea of ​​the chemical process. ConceptDraw DIAGRAM together with its Chemical and Process Engineering solution delivers the possibility to design Chemical Process Flow diagrams. It is designed for chemical industry engineers and designers.
"In mathematics, the Euclidean algorithm, or Euclid's algorithm, is a method for computing the greatest common divisor (GCD) of two (usually positive) integers, also known as the greatest common factor (GCF) or highest common factor (HCF). ...
The GCD of two positive integers is the largest integer that divides both of them without leaving a remainder (the GCD of two integers in general is defined in a more subtle way).
In its simplest form, Euclid's algorithm starts with a pair of positive integers, and forms a new pair that consists of the smaller number and the difference between the larger and smaller numbers. The process repeats until the numbers in the pair are equal. That number then is the greatest common divisor of the original pair of integers.
The main principle is that the GCD does not change if the smaller number is subtracted from the larger number. ... Since the larger of the two numbers is reduced, repeating this process gives successively smaller numbers, so this repetition will necessarily stop sooner or later - when the numbers are equal (if the process is attempted once more, one of the numbers will become 0)." [Euclidean algorithm. Wikipedia]
The flowchart example "Euclidean algorithm" was created using the ConceptDraw PRO diagramming and vector drawing software extended with the Mathematics solution from the Science and Education area of ConceptDraw Solution Park.
Euclid's algorithm flow chart
Euclid's algorithm flow chart, terminator, start, end, rectangle, process, action, decision, connector,
Used Solutions